不动点和蛛网图
B站:杨大师网课
不动点和蛛网图系列(共5节,不分p,是5个不同的视频)
目录
实数的不动点
相关概念
- 数列的生成函数
- 定义:也叫特征函数,an+1→y,an→x得到的函数
- 举例:an+1=an2,n∈N+⇒y=x2
- 数列的迭代
- 定义:根据初始值及递推关系逐一计算数列各项的过程(前一次计算时的 y 是后一次计算时的 x)
- 数列的不动点
- 定义:满足an+1=an,n∈N+的an的数值
- 举例:∵an+1=an2=an ∴am=0或an=1 ∴a1=0或1
- 补充
- 数列的“不动点”其实不是点,而是数值
- 若a1=不动点,则数列是常数数列,an=不动点
进一步分析
任何实数数列都有不动点吗?an+1=an2+8=an⇔an2−an+8=0⇒an无实数解
- 数列角度:\left\{\begin{align} &a_{n+1}=a_n \\ &a_{n+1}=a_n^2+b \end{align}\right.有解
- 函数角度:\left\{\begin{align} &y=x \\ &y=x^2+b \end{align}\right.有解
- 函数图像角度:
- 生成函数的图像与直线y=x有交点
- 生成函数图像与直线y=x的交点的横(纵)坐标=不动点
例题
例3、(2019浙江10改编)已知数列{an}满足a1=a,an+1=an2+6,n∈N+,则( )A.当b=21时,∀a∈R,a10>10恒成立C.当b=−2时,∀a∈R,a10>10恒成立B.当b=41时,∀a∈R,a10>10恒成立D.当b=−4时,∀a∈R,a10>10恒成立
易知:b=21时,无不动点b=41时,不动点21b=−2时,不动点−1或2b=−4时,不动点2−1±17(实际不用算,画图判断出不动点<10即可)
故排除BCD
而A易证其单调递增,a1=0时数列最小,递推(可用放缩简化计算量)后其成立
不动点的分类
当a1=1时,随着n增大an逐渐“远离”不动点,叫“排斥不动点”,如y=2xan逐渐“靠拢”不动点,叫“吸引不动点”,如y=21x
“蛛网图”的来历和本质
“蛛网图”来历和本质
迭代计算是一个代数运算的过程(前一步的y,是后一步的x);“蛛网图”是把迭代过程几何(图像)化处理
利用圆弧映射
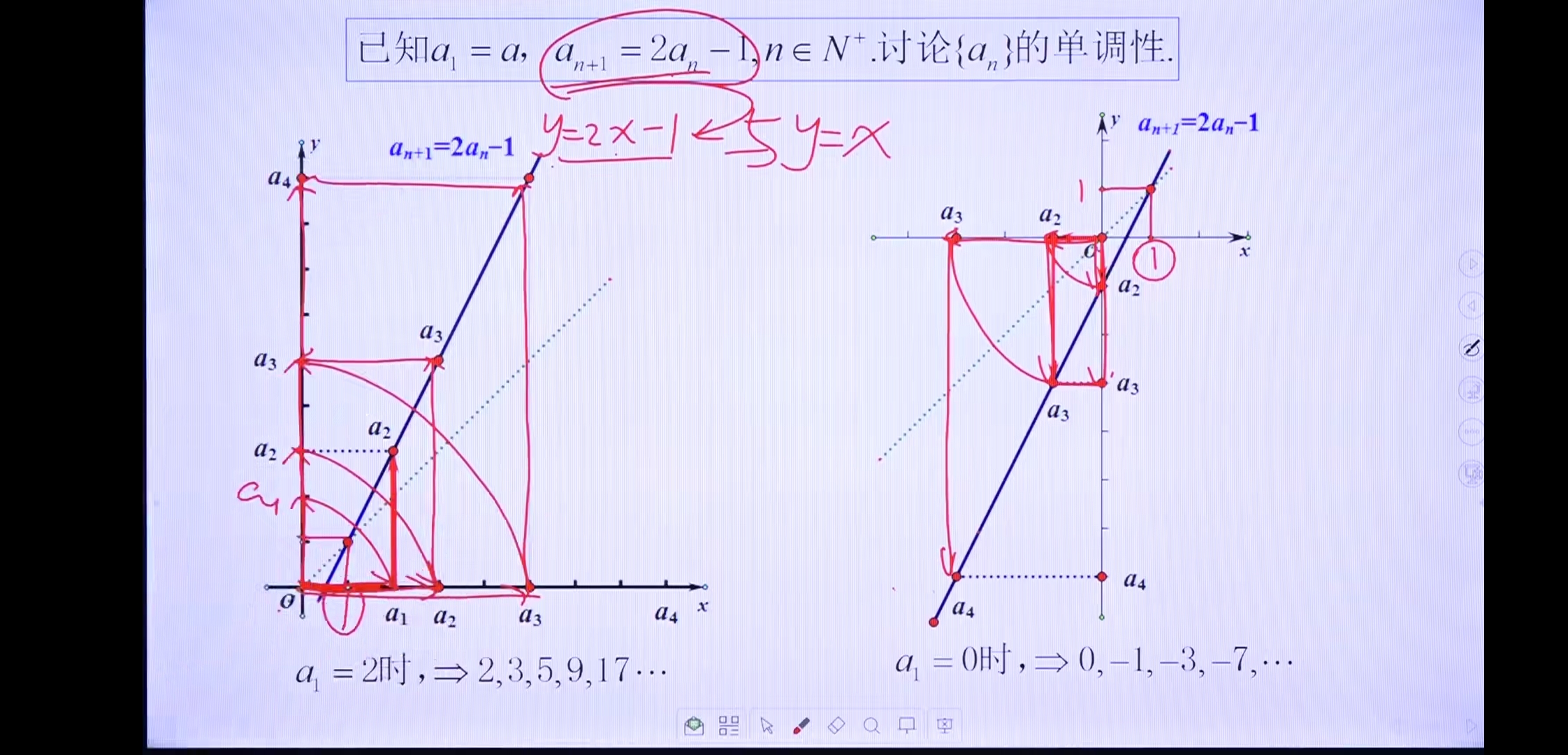
利用y=x映射
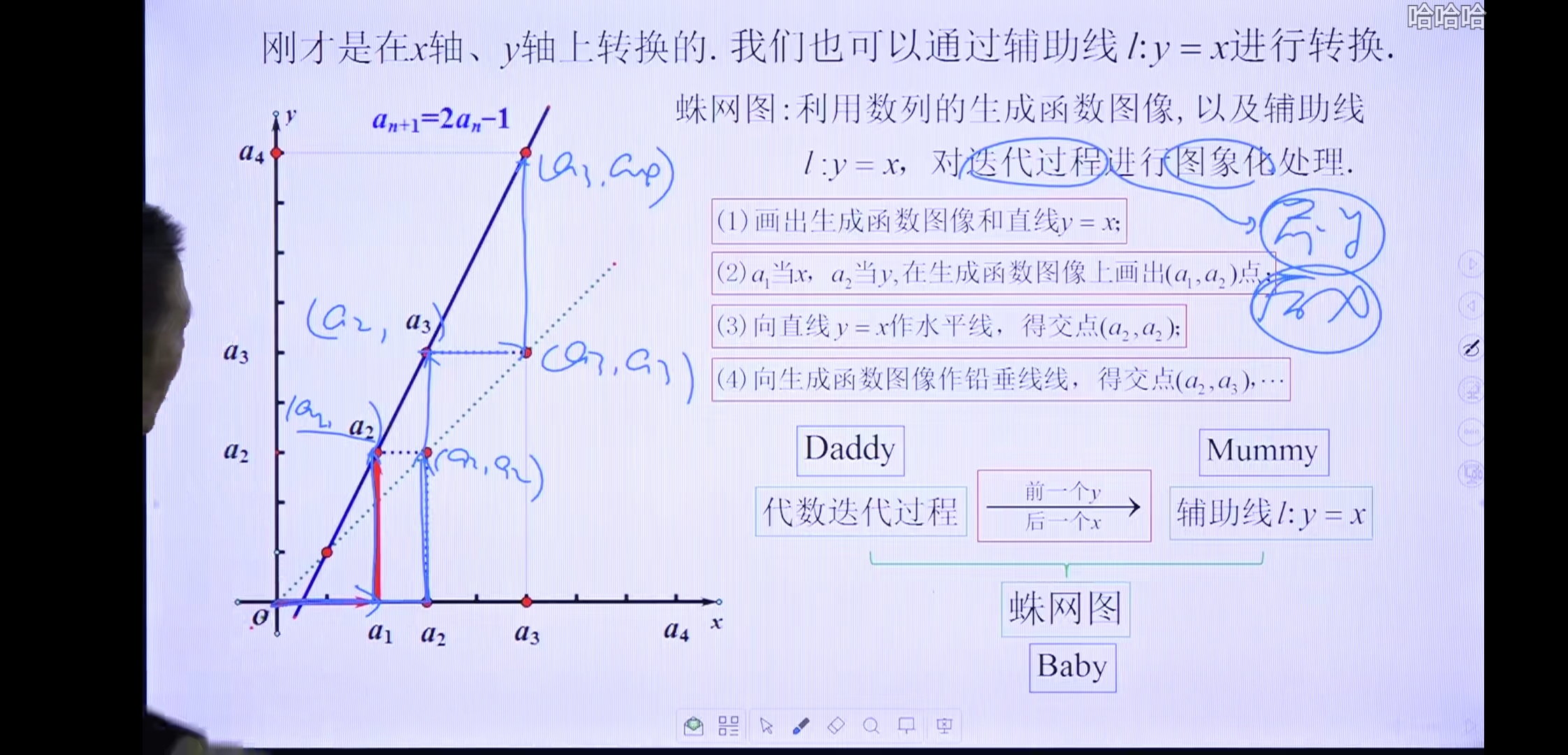
不动点类型和性质

吸引不动点(线性和振荡吸引)
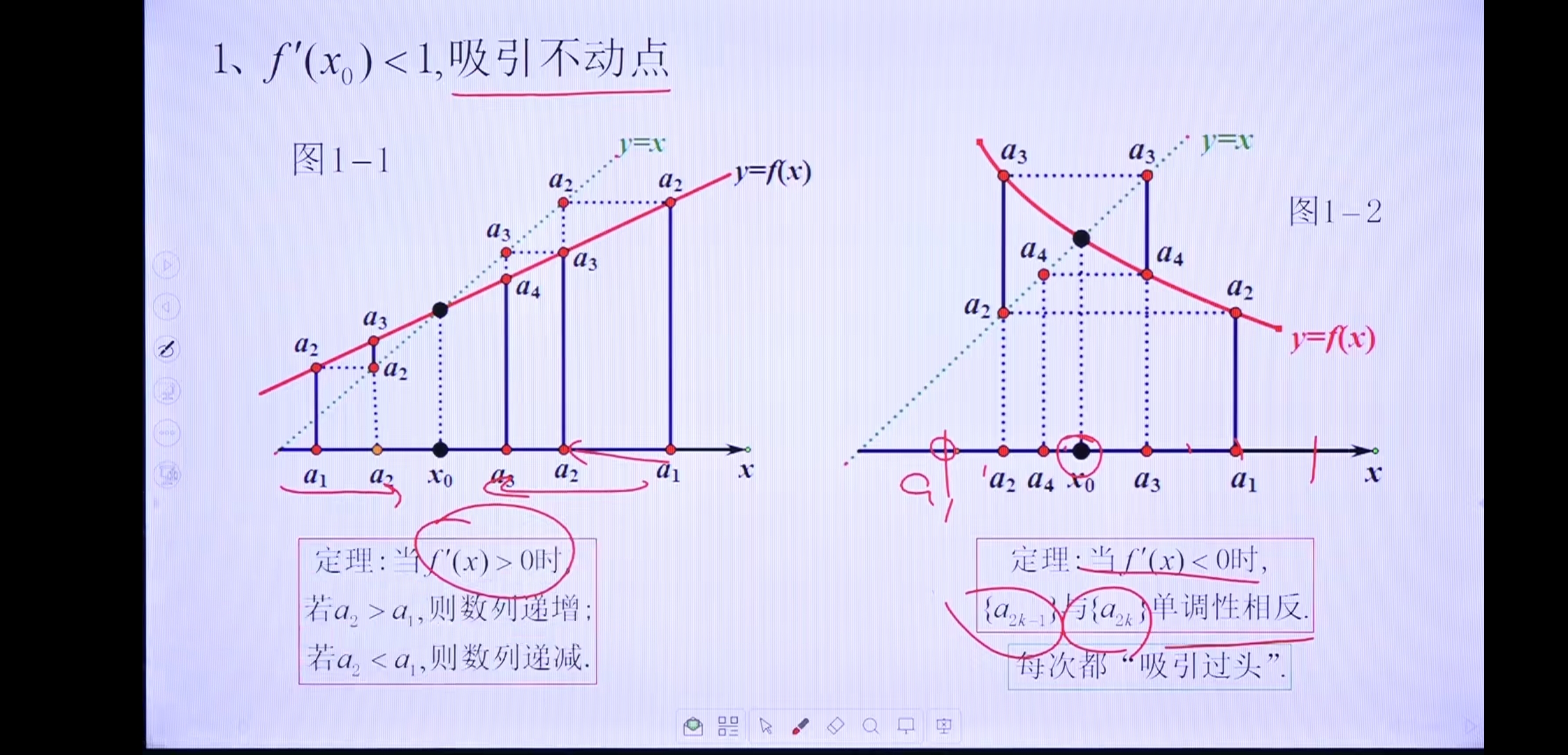
排斥不动点
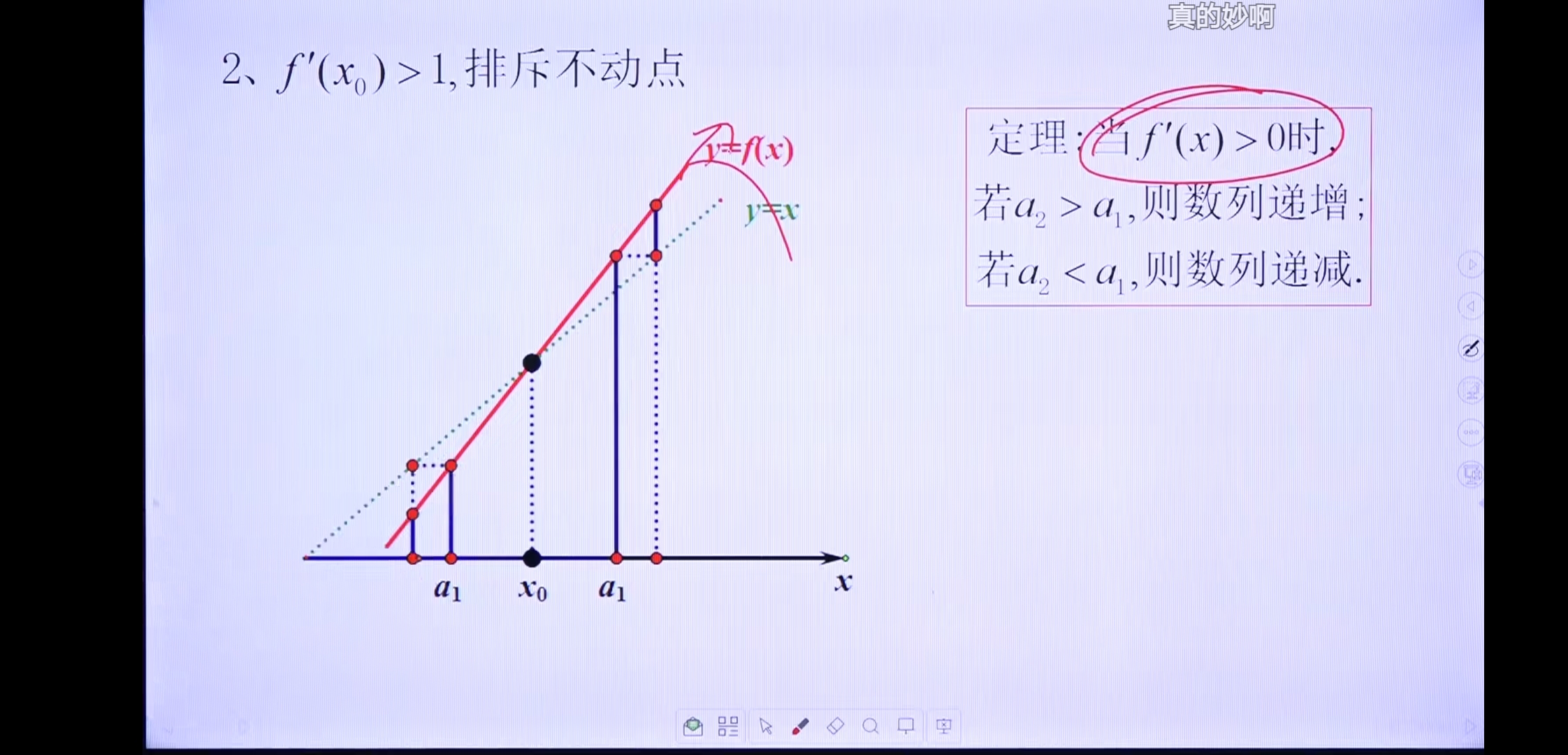
半吸半排不动点
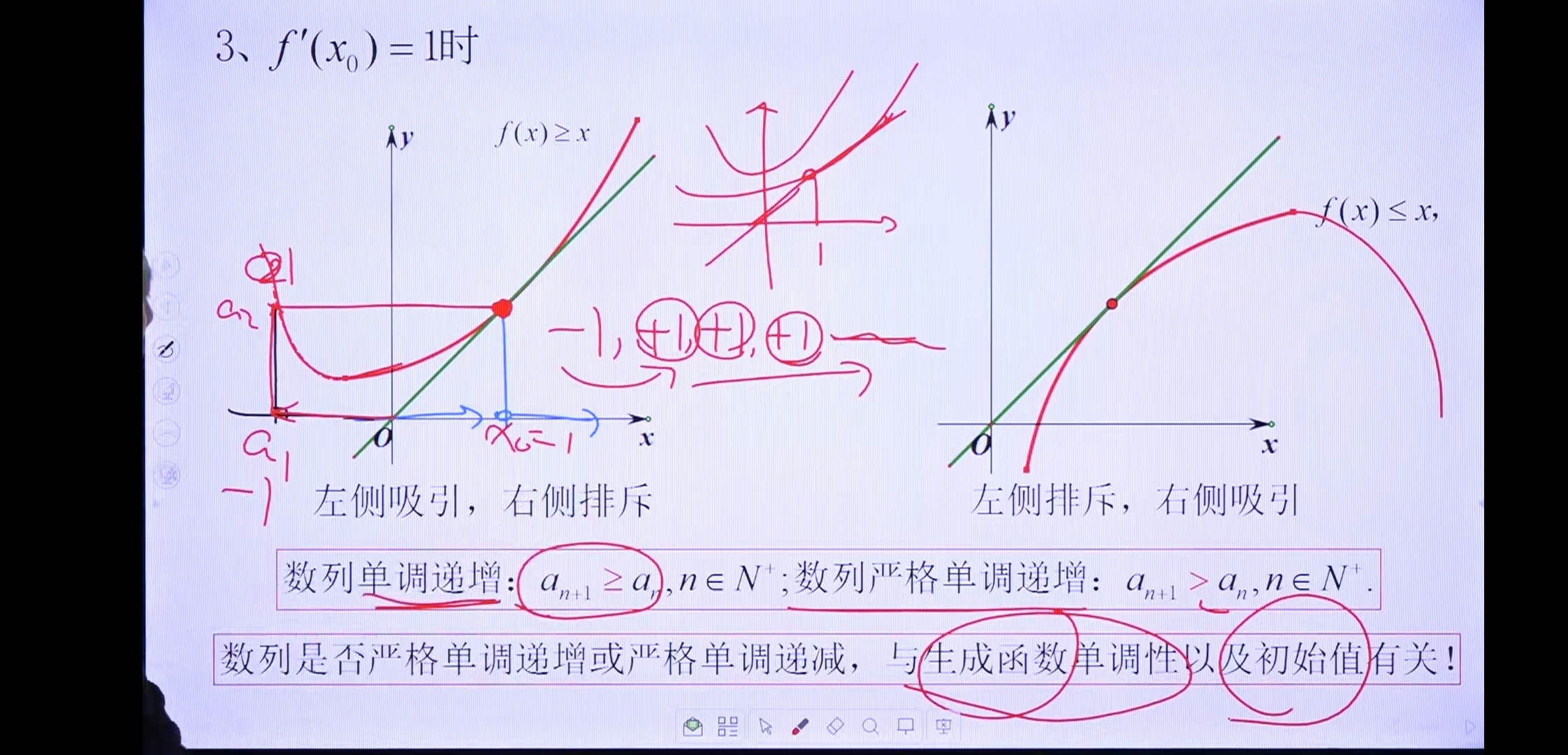
小结

个人总结
总之画图分析,简单明了不用记
- 不要记排斥和吸引,记向左还是向右
- 生长函数在y=x之上的,会往右
- 生长函数在y=x之下的,会往左
- 生长函数在y=x相交的,会不动
- 这样在生长函数与y=x有多个交点时,也成立
- 生长函数非单调时
- 有多种情况
- 间断点
- y′(x)>1>0时后变负数
- y′(x)<1时变负数
- 注意下,可能a2才停滞在不动点。或者a1到a2的递增的,后面都是递减
- 单调性改变的地方可能也需要分端看,特别是无穷间断点
- 相交与相切
蛛网图应用
应用
- 【应用1】判定数列的单调性和极限
- 【应用2】已知数列的生成函数及单调性,求a1的取值范围
- 【应用3】已知数列单调性,求生成函数中的参数范围(生成函数图不确定,难度稍大)
- 【应用4】判定an+1与kan+b的大小关系(映射辅助线不确定,难度稍大)
例题
易错:刚开始的的a1是在x轴上
应用1
例1
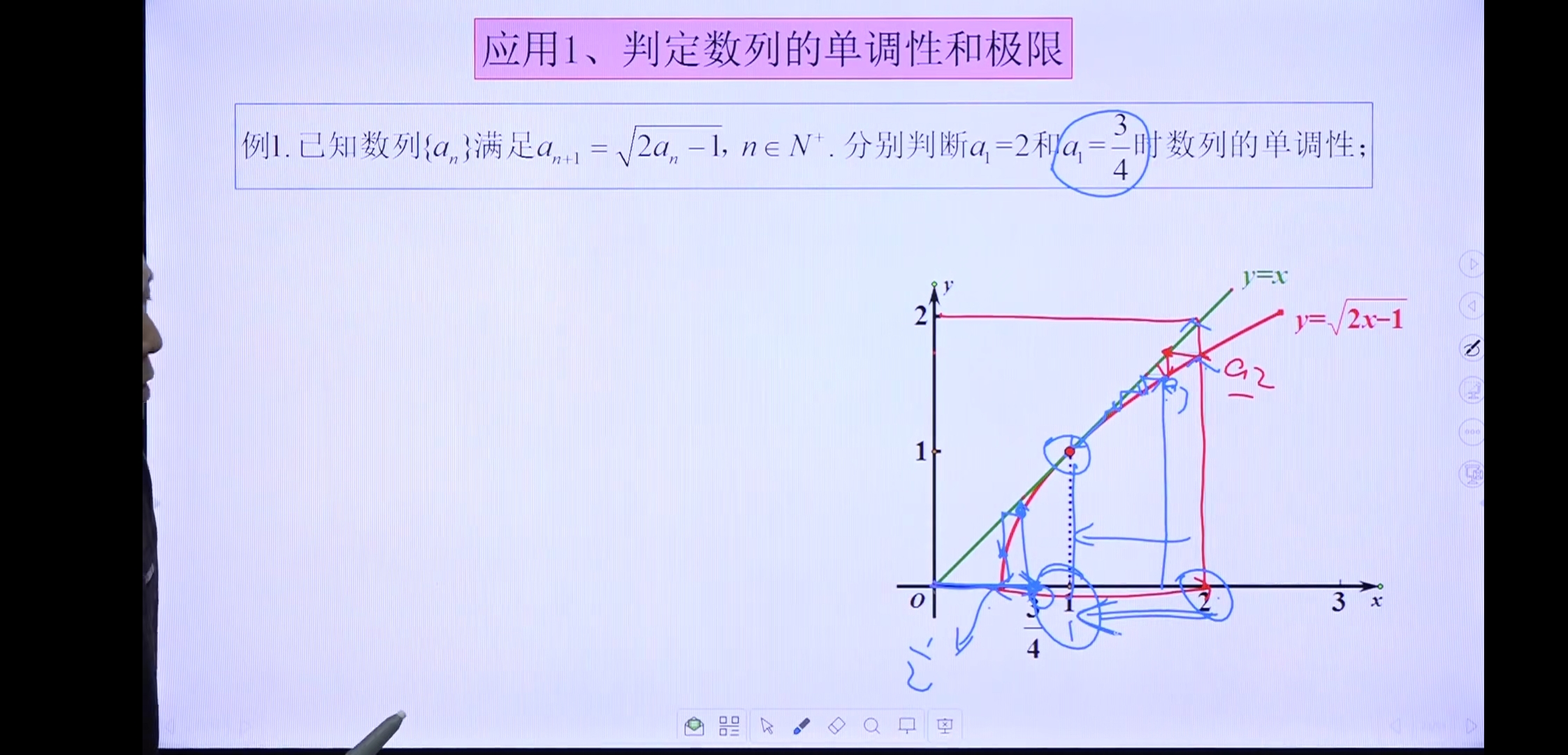
例2
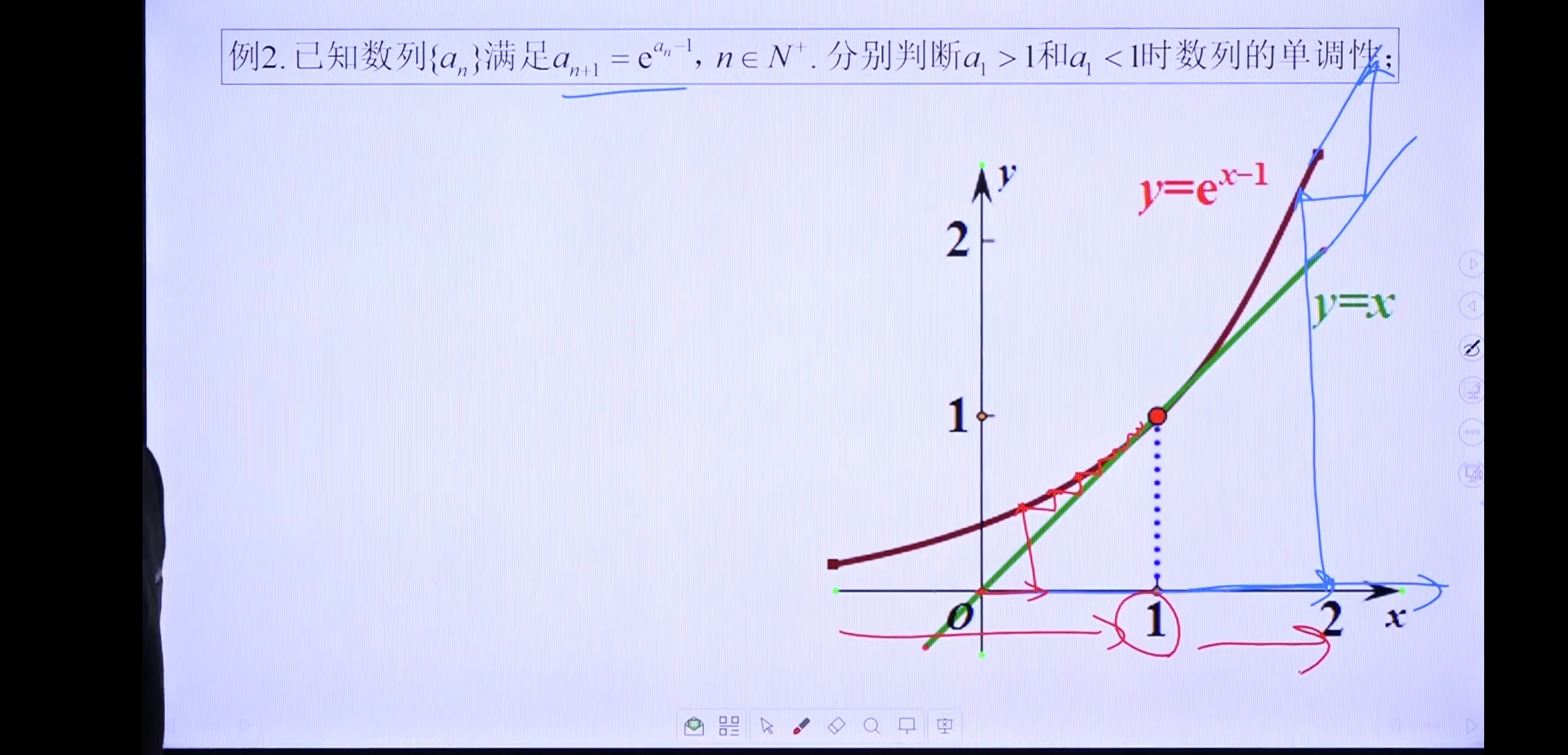
例3
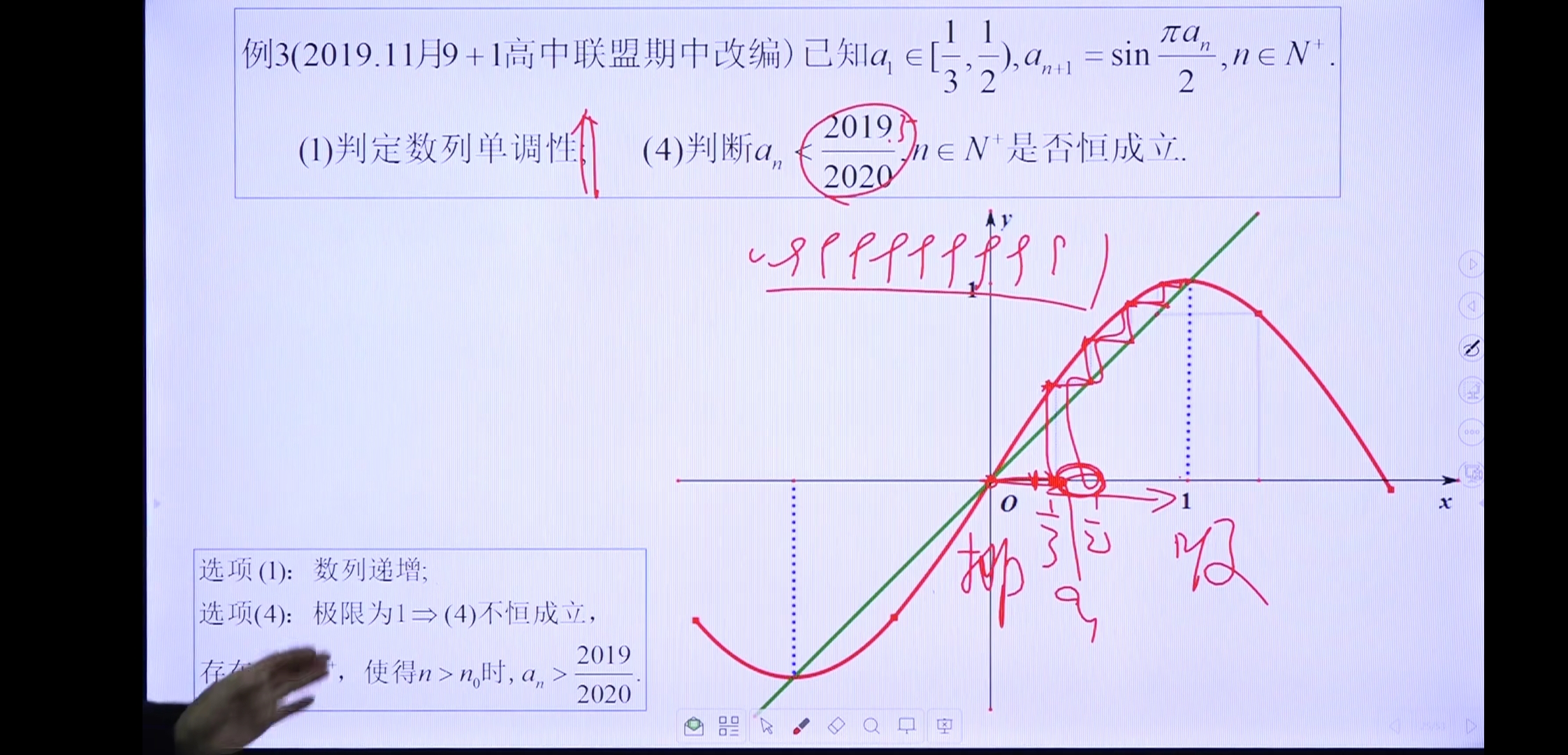
应用2
例1
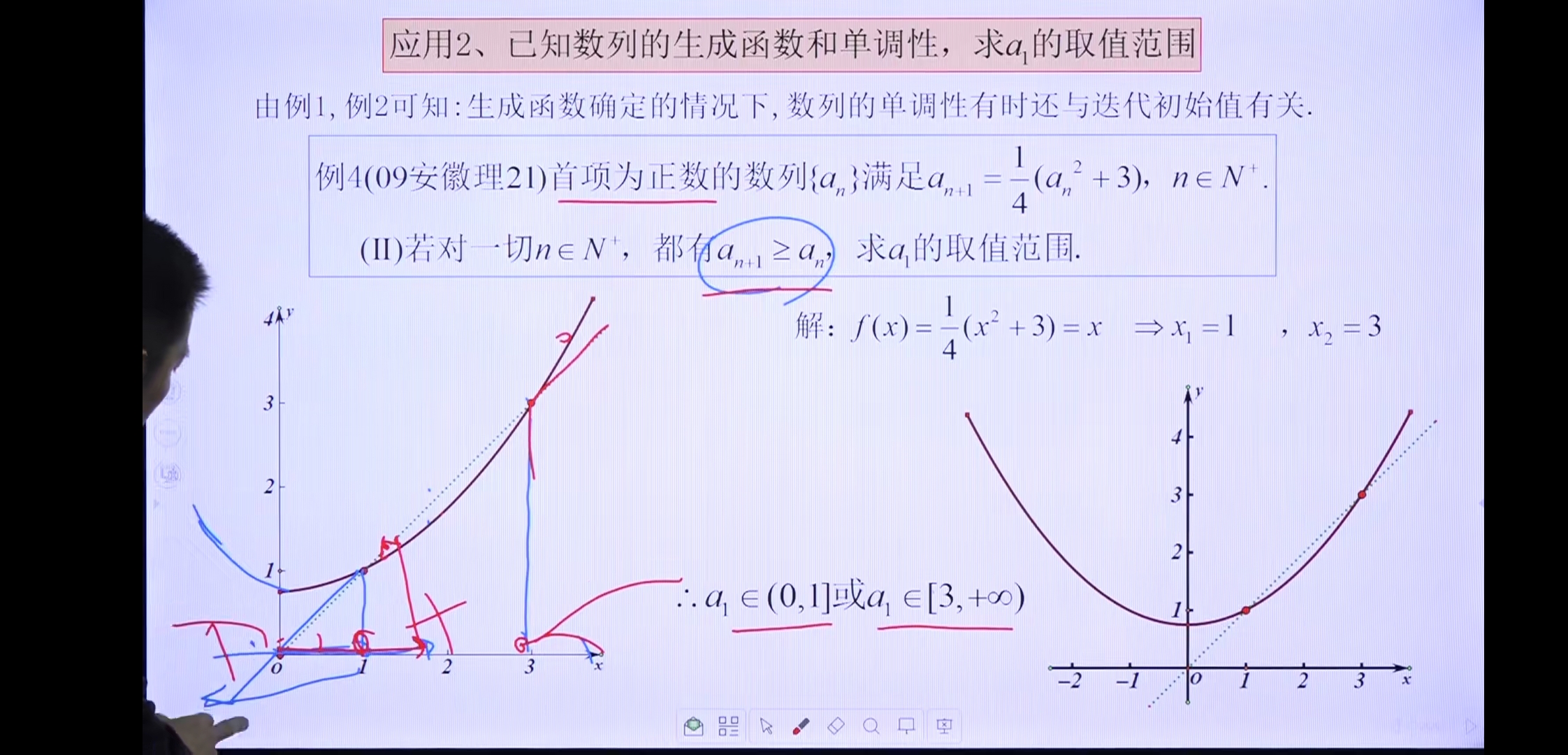
例2
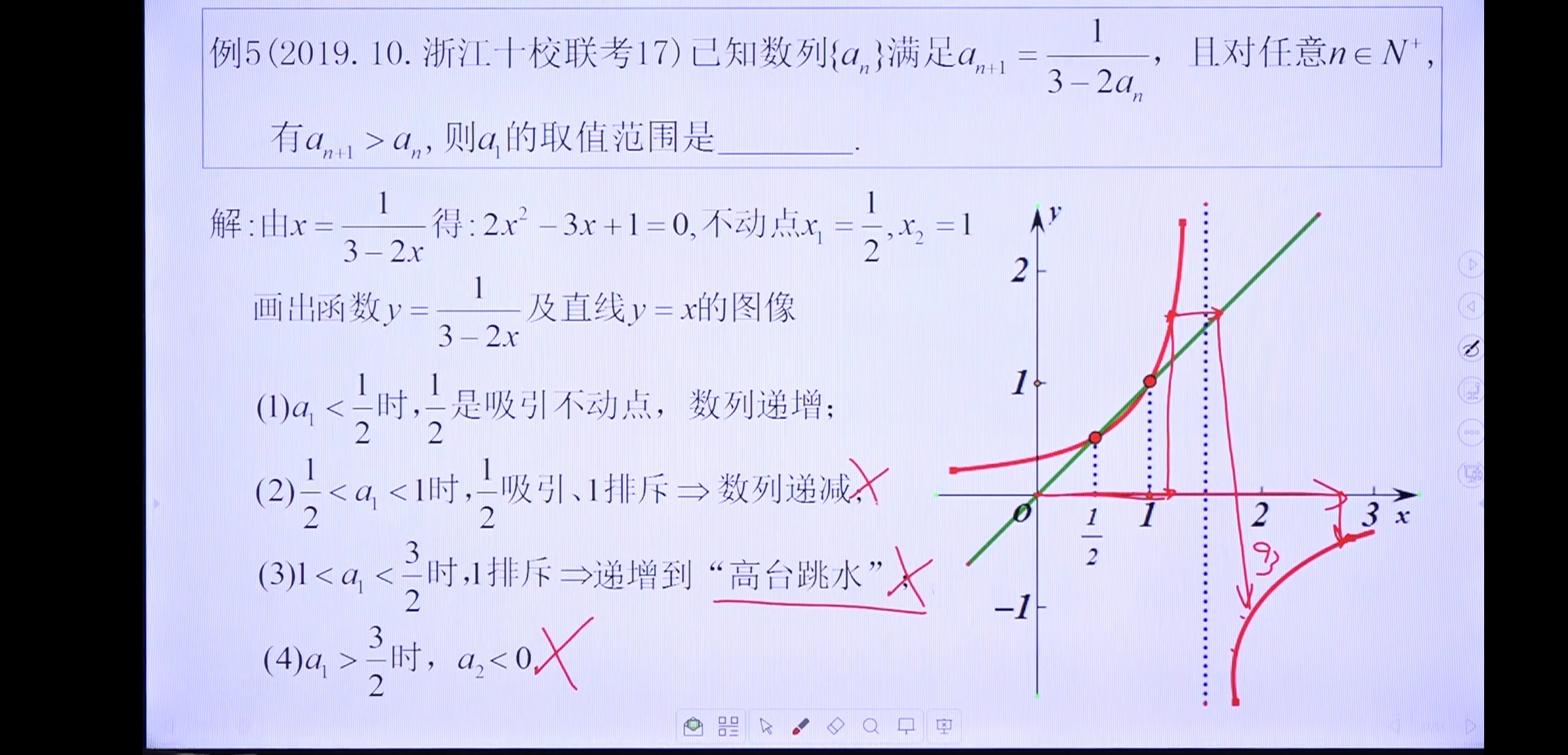
例3
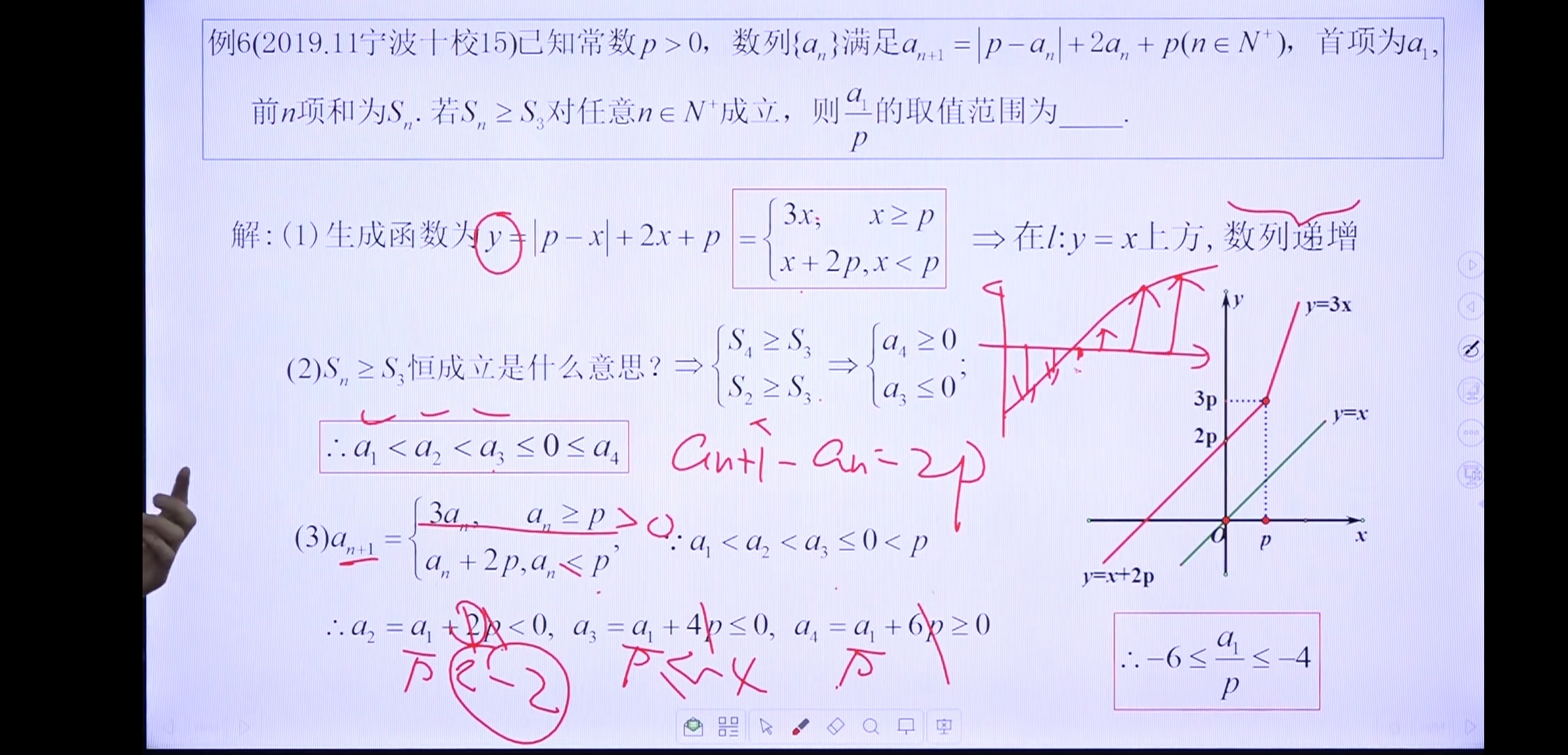
小结

应用3
例1(!)

例2

例3
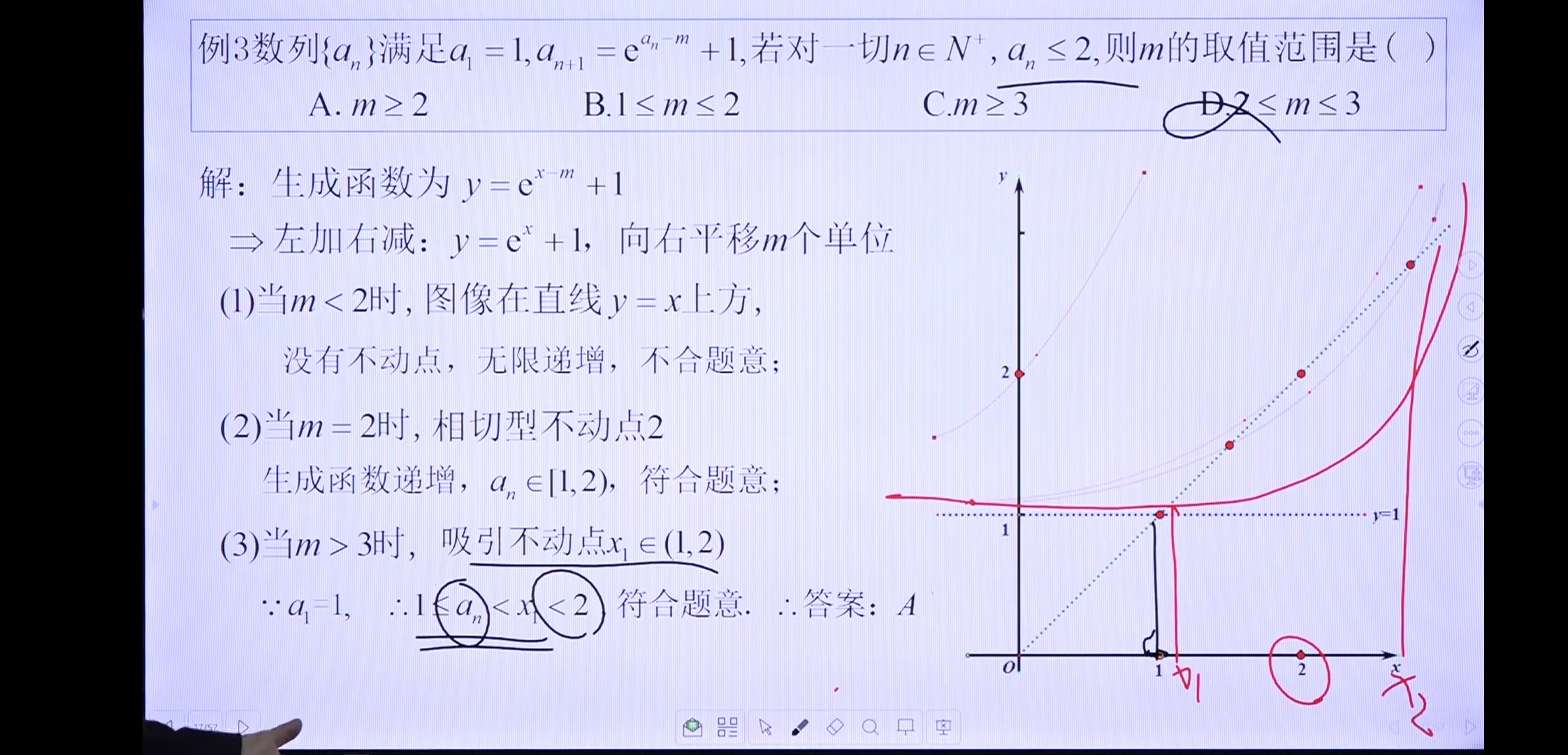
例4(!)
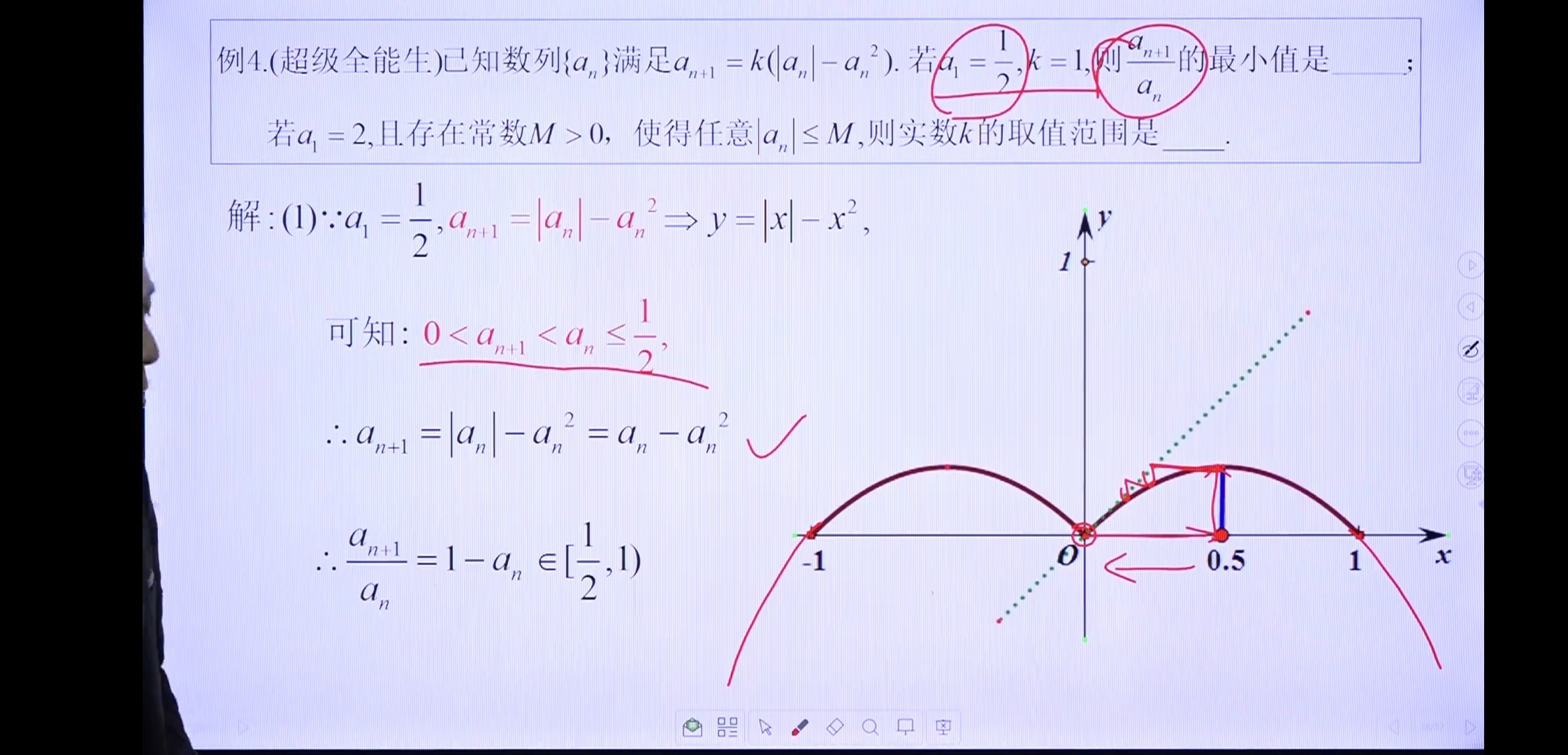
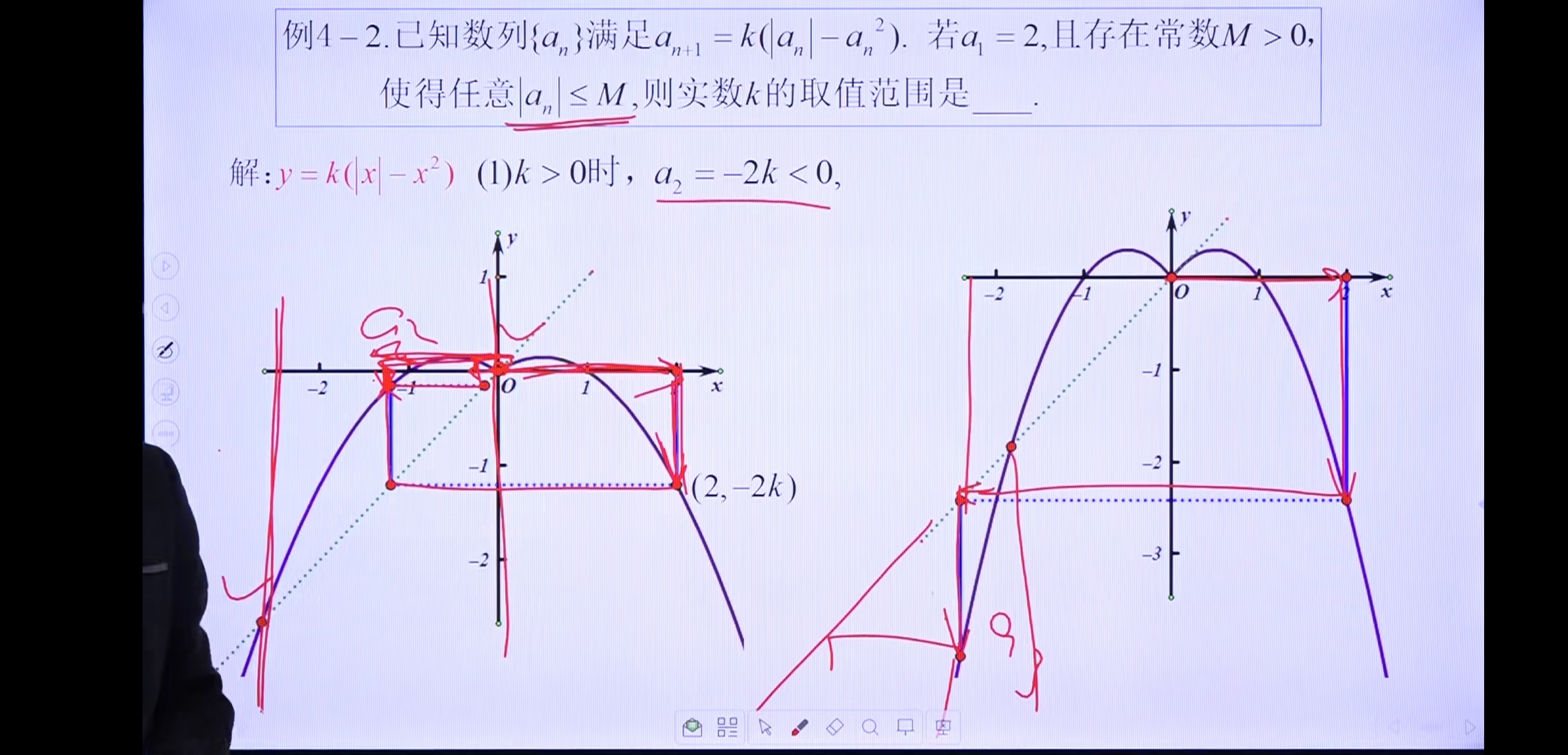

思考
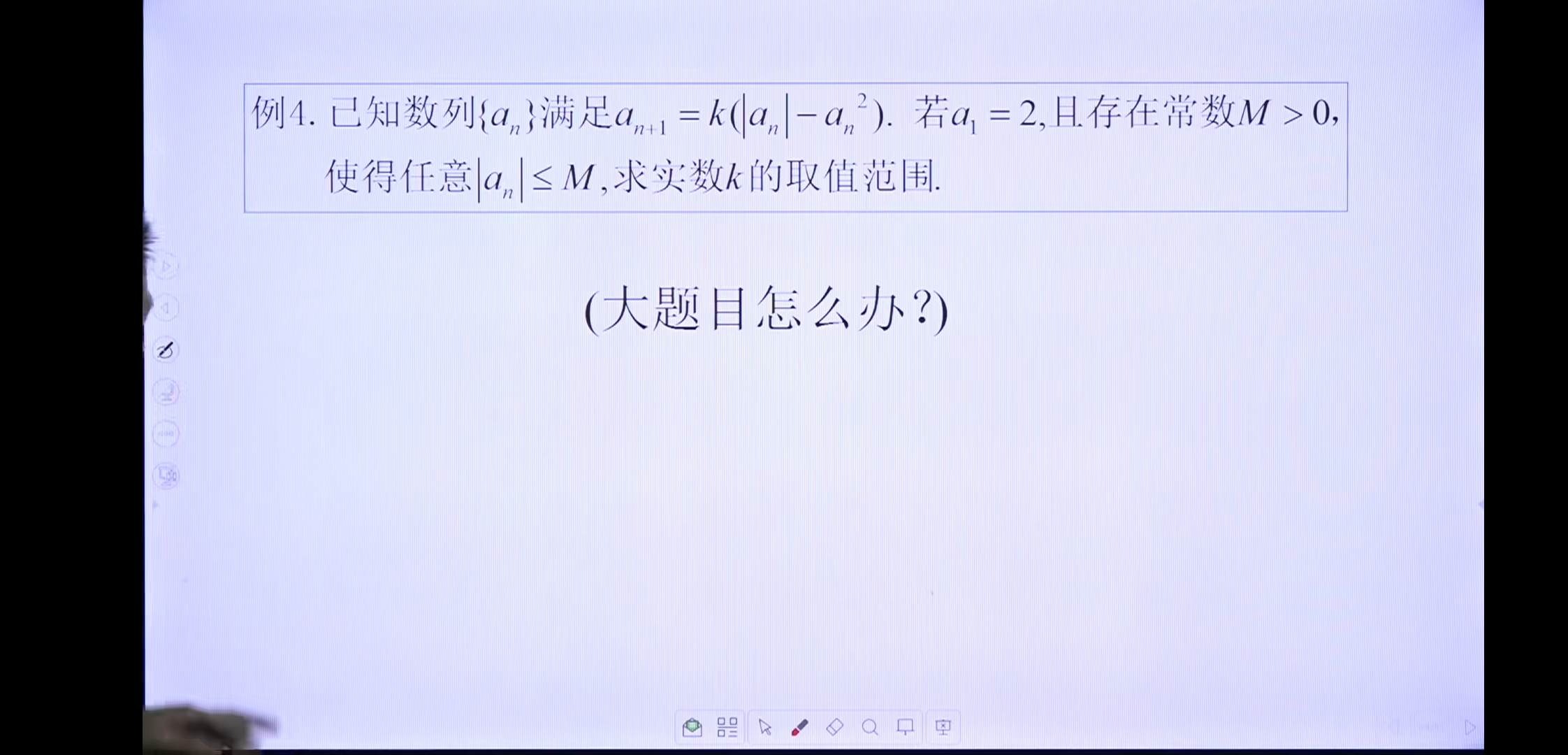
应用4
略




















